Langkah Umum Principal Component Analysis

Misalkan kita memiliki sebuah balok dengan informasi panjang (p), lebar (l) dan tinggi (t). Dari ketiga jenis infomasi ini, bila kita olah dan kita ganti dengan  informasi volume (v) dari balok tersebut, maka informasi volume dianggap sudah dapat menggambarkan panjang, lebar dan tinggi balok tadi. Karena v = p x l x t.
Inilah konsep sederhana kinerja Principal Component Analysis.

PCA bekerja pada data set ukuran besar (mxn) dan kemudian mentransformasinya ke ukuran (mxk) dengan mempertahankan data yang tidak redundant, atau tidak berkorelasi, atau tidak berhubungan. Kenapa data yang tidak berkorelasi? sebab data-data inilah yang memiliki peran penting terhadap variasi data asli.

Kembali lagi ke ilustrasi balok tadi. Seandainya informasi yang kita miliki adalah p, l, t, v dan 2v. Dalam hal ini 2v adalah 2 x volume. Nah 2v inilah yang saya maksud data yang redundant. Informasi 2v bisa didapatkan hanya dengan menyimpan data v saja. Sedangkan p, l dan t berkorelasi dengan nilai v. Jadi dari p, l, t, v dan 2v…cukup disimpan nilai v-nya saja.

Apakah korelasi (correlation), dan bagaimana cara menghitung korelasi? jawabannya ada di catatan saya di sini. Singkatnya, dengan mengetahui korelasi antara dua variabel, misal korelasi p terhadap l, t terhadap p, 2v terhadap v dapat menjadikan dasar dimulainya proses PCA.

Korelasi sendiri tidak dapat dilepaskan dari saudaranya…yaitu kovarians. Catatan saya mengenai kovarians dapat dilihat di sini.

Terdapat banyak cara merepresentasikan hubungan antara dua atau beberapa variabel dengan melihat perubahan nilainya. Contohnya dengan grafik linear, eksponensial, periodic, log..dsb. PCA menggunakan grafik linear dan basisnya adalah nilai korelasi.

Untuk lebih jelasnya, saya coba jelaskan proses PCA dimulai dengan langkah umum diikuti penjelasan beserta contoh program menggunakan Matlab.

Langkah umum penyelesaian PCA dapat dilihat pada diagram berikut:

Gambar 1. Langkah PCA

(warna hijau menandakan program yang ditulis dalam Matlab)

1. Input data

Data awal dipersiapkan dalam sebuah matriks ukuran mxn. Nantinya jumlah variable n akan berkurang menjadi k jumlah principal component yang dipertahankan.

Contoh data yang diinputkan adalah:

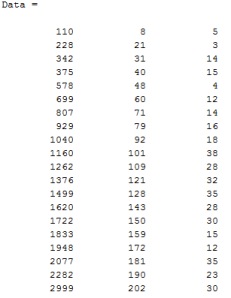
Sebut saja kolom pertama adalah variabel X, kedua Y dan ketiga Z. Masing-masing barisnya (observasi) diberi label: a, b, c…dan seterusnya sampai t. Tabel Data berukuran 20×3. Dengan m=20 dan n=3.

X dengan range 110-2999, Y: 8-202 dan Z: 5-30.
_________________________________

Data =[110 8 5; 228 21 3; 342 31 14; 375 40 15; 578 48 4; 699 60 12; 807 71 14; 929 79 16; 1040 92 18; 1160 101 38; 1262 109 28; 1376 121 32; 1499 128 35; 1620 143 28; 1722 150 30; 1833 159 15; 1948 172 12; 2077 181 35; 2282 190 23; 2999 202 30];
plot3(Data(:,1),Data(:,2),Data(:,3),’o’)
labels=’abcdefghijklmnopqrst’;
labels = labels’;
text(Data(:,1), Data(:,2), Data(:,3), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘X’);
ylabel(‘Y’);
zlabel(‘Z’);
_________________________________

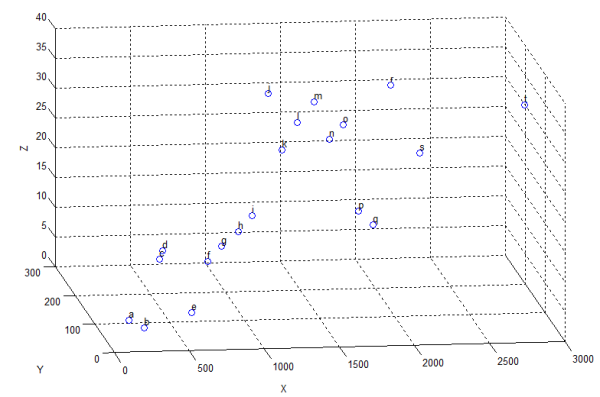
Gambar 2. Grafik data awal

Bila kita perhatikan hubungan antara variabel X dan Y, X dan Z serta Y dan Z seperti berikut:

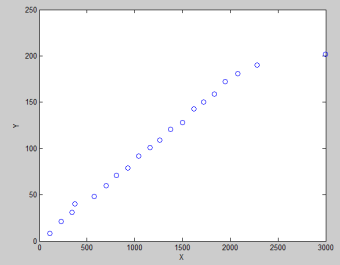
Gambar 3. Hubungan antara variabel X dan Y

Terlihat  bahwa variabel X dan Y terhubung secara linear. Kelihatannya perubahan pada satu variabel berarti juga perubahan pada variabel lainnya. Walaupun besarnya perubahan tidak sama. Ini dikarenakan unit/satuan atau range yang berbeda (lihat tabel Data).

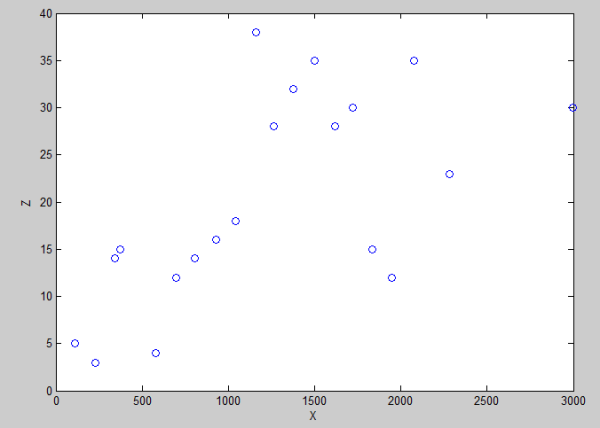
Gambar 4. Hubungan antara variabel X dan Z

Sedangkan pada Gambar 4 dan 5, perubahan nilainya ‘seperti’ tidak berhubungan secara linear.

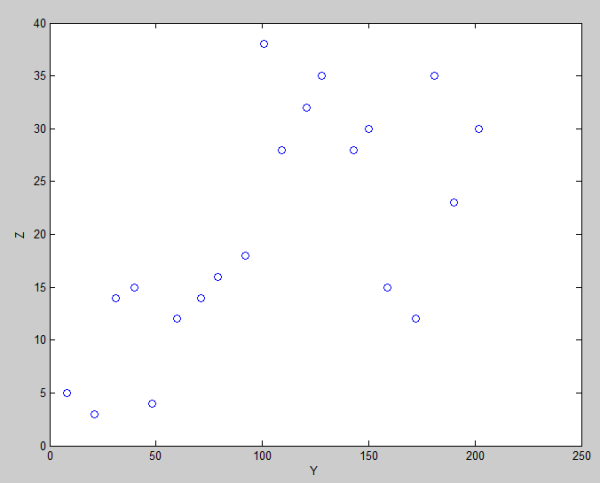
Gambar 5. Hubungan antara variabel Y dan Z

Satuan ataupun range yang berbeda tentu saja tidak dapat dibandingkan. Misalkan satuan Kilometer tidak dapat dibandingkan dengan satuan Celcius atau Tinggi badan seseorang tidak dapat dibandingkan dengan nilai raportnya.

Nah, dengan keadaan data yang seperti ini..sebaiknya dilakukan langkah standarisasi agar variabel-variabelnya layak untuk dibandingkan.

2. Pre-PCA

Cara standarisasi adalah dengan menggunakan Z-Score.

Cara menghitungnya adalah dengan:

dimana:

z: nilai standard score, x: data observasi, μ: mean per variabel dan σ: standar deviasi per variabel. Hasil dari Z-score ini adalah data dengan  mean = 0 dan standar deviasi = 1.

Sederhananya, proses Z-score: tiap data observasi pada sebuah variabel dikurangi dengan mean variabel tersebut dan dibagi dengan standar deviasinya (dengan kata lain, tiap baris per kolom dikurangi mean kolom tersebut, dibagi dengan standard deviasi kolom yang sama).

Data awal yang sudah distandarisasi adalah:

_________________________________
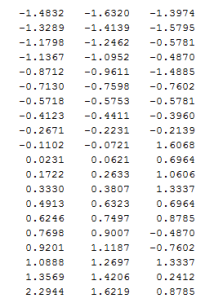
%standarisasi data
DatStd=zscore(Data);
hold on;
figure(‘name’,’Standardized Data’);
plot3(DatStd(:,1),DatStd(:,2),DatStd(:,3),’o’)
text(DatStd(:,1), DatStd(:,2), DatStd(:,3), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘X’);
ylabel(‘Y’);
zlabel(‘Z’);
_________________________________

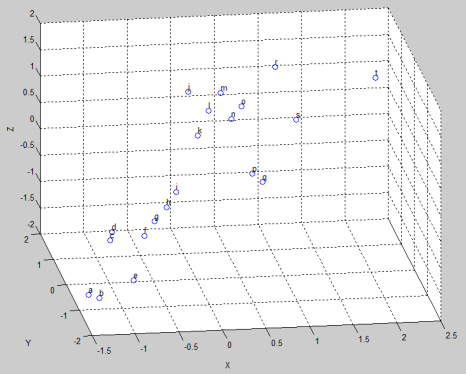
Gambar 6. Hasil Standarisasi

dari hasil standarisasi dapat dilihat sekarang data sudah comparable, berada pada range yang hampir sama dan dengan unit (deviasi) yang sama pula. Dengan mean=0 pada variabel X, Y dan Z sebagai pusat koordinat.

Langkah berikutnya adalah memproses KORELASI dari data.
Perlu dicatat bahwa hasil korelasi dari data yang tidak distandarisasi adalah sama dengan hasil kovarians dari data yang distandarisasi.

Nah, karena data sudah distandarisasi, sekarang kita lanjut dengan memproses covariance-nya saja. Hasilnya adalah:

 1.0000    0.9831    0.6250
0.9831    1.0000    0.6482
0.6250    0.6482    1.0000

Ukuran matriks covariance adalah nxn (dalam hal ini 3×3), sesuai dengan jumlah variabel yang ada. Sesuai dengan penjelasan saya pada catatan tentang covariance, data pada kolom ke-1 baris ke-1 adalah variance variabel X dengan dirinya sendiri. Nilainya 1. Obvious! Perhatikan Gambar 7.

Oh ya, di atas sudah disebutkan bahwa hasil covariance ini sama dengan hasil korelasi. Jadi bisa juga kalau saya sebutkan matriks covariance di atas adalah matriks korelasi. Korelasi X terhadap dirinya sendiri adalah korelasi sempurna positif. Ini juga obvious! Sama halnya dengan kolom 2 baris 2 (Y dengan dirinya sendiri) dan kolom 3 baris 3 (Z dengan dirinya sendiri).

Kemudian dari hasil matriks yang sama, korelasi antara variabel X terhadap Y terlihat mendekati sempurna: tinggi positif. Yang artinya X dan Y mendapatkan perubahan ke arah yang sama. Bila X berubah ke arah positif, demikian halnya dengan Y. Perhatikan Gambar 8.

Sedangkan Korelasi antara X dan Z, mirip dengan korelasi Y dan Z. Korelasinya positif namun sedang-sedang saja. Perhatikan Gambar 9 dan 10.

_________________________________
%menghitung covarians dari data yang sudah distandarisasi
C=cov(DatStd);
hold on;
figure(‘name’,’Covariance between X and X’);
plot(DatStd(:,1),DatStd(:,1),’o’);
text(DatStd(:,1), DatStd(:,1), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘X’);
ylabel(‘X’);
_________________________________

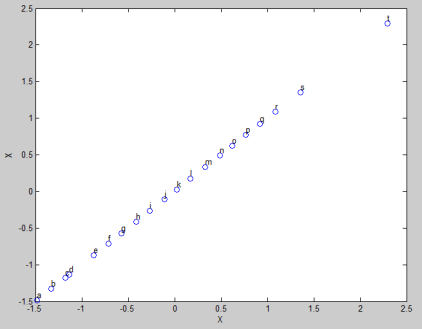
Gambar 7. Covariance antara variabel X dan X

_________________________________
hold on;
figure(‘name’,’Covariance between X and Y’);
plot(DatStd(:,1),DatStd(:,2),’o’);
text(DatStd(:,1), DatStd(:,2), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘X’);
ylabel(‘Y’);
_________________________________

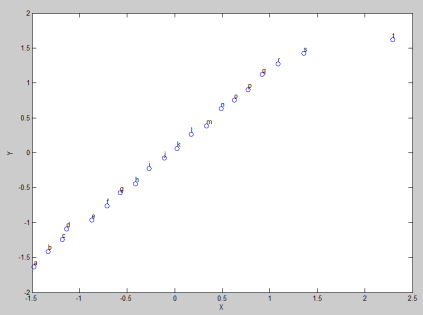
Gambar 8. Covariance antara variabel X dan Y

_________________________________
hold on;
figure(‘name’,’Covariance between X and Z’);
plot(DatStd(:,1),DatStd(:,3),’o’);
text(DatStd(:,1), DatStd(:,3), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘X’);
ylabel(‘Z’);
_________________________________

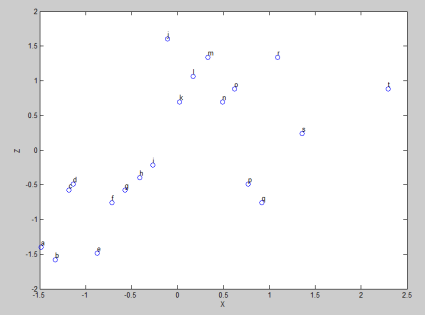
Gambar 9. Covariance antara variabel X dan Z

_________________________________
hold on;
figure(‘name’,’Covariance between Y and Z’);
plot(DatStd(:,2),DatStd(:,3),’o’);
text(DatStd(:,2), DatStd(:,3), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘Y’);
ylabel(‘Z’);
_________________________________

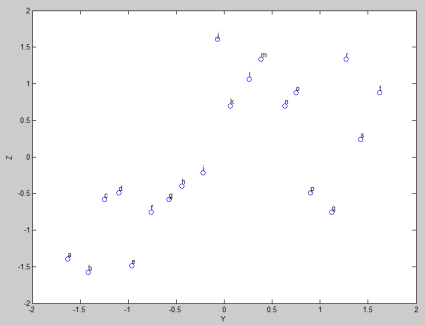
Gambar 10. Covariance variabel Y dan Z

3. Proses PCA

Berikutnya adalah inti dari pembahasan kita, yakni PCA. Yang kita harapkan dari hasil langkah 2 di atas, adalah:

• sebuah transformasi linear yang dilakukan menggunakan koordinat sistem yang baru (principal component terpilih), dan
• sumbu-sumbu koordinat baru ini nantinya harus orthogonal (saling tegak lurus) karena mangandung informasi variabel yang tidak saling berkorelasi (ini sebabnya PCA diawali dengan langkah menghitung Korelasi).
• Jumlah principal component yang dipilih adalah dimensi dari koordinat yang baru.
• Masing-masing sumbu koordinat yang dipilih harus meminimalisir jumlah dari kuadrat error dari sumbu tersebut ke setiap data point (lihat absolute error pada catatan saya di sini).

Nah, untuk dapat mentransformasi dari data asal ke variabel yang saling tidak berkorelasi, adalah dengan menggunakan eigenvector dari matriks korelasi.

Cara menentukan eigenvector (tentu saja tidak lepas dari nilai eigenvalue-nya) dapat dilakukan dengan 2 cara, yaitu: Eigenvalue Decompisition atau Singular Value Decomposition. Catatan saya mengenai kedua hal ini dapat dilihat di: EVD dan SVD

Dalam contoh kali ini saya menggunakan EVD, karena hasil matriks covariance yang sudah saya standarisasi adalah matriks simetris.
_________________________________
%eigen value decomposition
[V,D] = eig(C);
%ubah letak eigenvektor berdasarkan eigenvalue (descending order)
D2=diag(sort(diag(D),’descend’));
[c, ind]=sort(diag(D),’descend’);
V2=V(:,ind);
figure(‘name’,’principal component plot’)
plot3(DatStd(:,1), DatStd(:,2),DatStd(:,3), ‘o’);
text(DatStd(:,1), DatStd(:,2),DatStd(:,3), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
hold all
plot3(V2(1,1)*[-5 5], V2(2,1)*[-5 5], V2(3,1)*[-5 5], ‘-r’)
hold all
plot3(V2(1,2)*[-2 2], V2(2,2)*[-2 2], V2(3,2)*[-2 2], ‘-r’)
xlabel(‘X’);
ylabel(‘Y’);
zlabel(‘Z’);
_________________________________

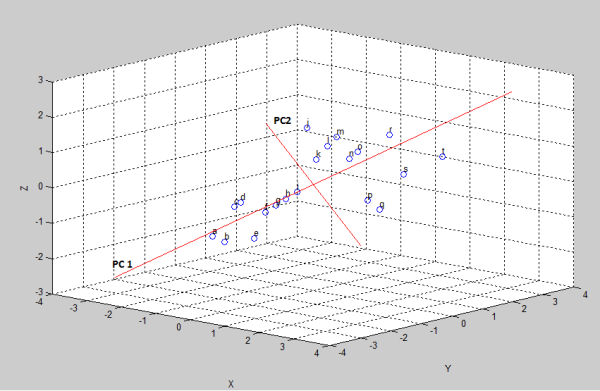
Gambar 11. Plotting Principal Component, PC1 dan PC2

Dari hasil EVD: eigenvektor dengan nilai eigenvalue tertinggi meng-capture variasi data tertinggi.

Biasanya untuk PCA yang bekerja dengan baik, 2 principal component yang dipilih dari 2 eigenvektor dengan eigenvalue tertinggi sudah mampu meng-capture 50% dari total variasi data. (Dalam contoh ini, saya pilih 2 PC saja).

Perhatikan Gambar 11. Kedua principal component yang terpilih (warna merah) saling tegak lurus satu sama lain dan dapat dilihat melalui grafik yaitu setiap sumbu yang baru (PC1 & PC2) berjarak dekat (bila ditarik garis tegak lurus) dengan setiap data point (ingat: ‘masing-masing sumbu koordinat yang dipilih harus meminimalisir jumlah dari kuadrat error dari sumbu tersebut ke setiap data point‘).

Karena 2 principal component yang terpilih, maka k=2.

4. Output

_________________________________
figure(‘name’,’axis changed based on principal components’)
PcaPos = DatStd * V2(:, 1:2);
plot(PcaPos(:,1),PcaPos(:,2),’o’);
text(PcaPos(:,1),PcaPos(:,2), labels, ‘horizontal’,’left’, ‘vertical’,’bottom’);
xlabel(‘PC1’);
ylabel(‘PC2’);
_________________________________

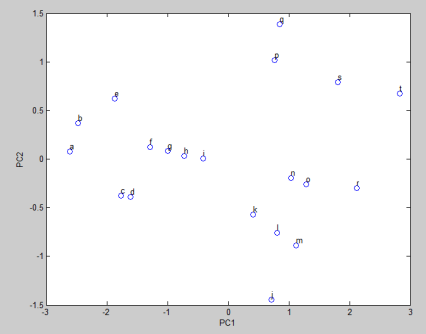
Gambar 12. Hasil transfromasi data terhadap koordinat (axis) baru, PC1 dan PC2

Perhatikan Gambar 12. Dari kedua principal komponen yang terpilih, kemudian dilakukan transformasi dengan PC1 dan PC2 sebagai sumbu koordinat kita yg baru. Transformasinya: Data yang telah distandarisasi (m x n) dikalikan dengan principal component yang terpilih (n x k) menghasilkan sebuah matriks hasil transformasi berukuran  m x k. Dalam contoh ini: 20 x 2.

Dari hasil transformasi ini, PC1 dan PC2 telah dirotasi menjadi sumbu dari koordinat baru untuk transformasi data.

Proses PCA telah men-reduce ukuran matriks asal m x n ke ukuran m x n dengan tetap mempertahankan variasi data, yaitu data yang tidak redundan/tidak berkorelasi.

Selesai.

Contoh penggunaan PCA yang saya buat dengan memanfaatkan fungsi princomp matlab dapat dilihat di sini.

Mudah-mudahan catatan ini bermanfaat.

Salam.